 カワセミ@金融ブロガー
カワセミ@金融ブロガーこんにちは。カワセミ@金融ブロガーです
特徴量(Feature)とは、機械学習モデルに入力されるデータの要素であり、モデルが現実世界を理解し予測を行うための「言語」や「語彙」のような存在です。
たとえば、住宅価格を予測するタスクでは「立地」「築年数」「部屋数」「面積」といった情報が特徴量となり、これらを適切に設計できるかどうかが予測精度を大きく左右します。モデルの選定やハイパーパラメータ調整も重要ですが、実際にはどんな特徴量を与えるかによって性能が決まることが多く、データサイエンティストにとって最も創造的であり、かつ重要な作業のひとつといえます。
特徴量設計が不十分な場合、どれほど高度なアルゴリズムを使っても精度は伸び悩みます。逆に、シンプルなモデルでも良質な特徴量が揃っていれば、予測精度や再現性は大きく改善し、モデルの解釈性や運用コストの削減にもつながります。そのため、特徴量は「モデルの性能を決定づける最重要要素」として多くの研究や実務で注目されています。
本記事では、まず直感的な定義と特徴量の役割を整理したうえで、評価指標への影響や設計の基本フローを解説します。
これから機械学習を学ぶ初心者はもちろん、既にモデル構築の経験があるエンジニアやデータアナリストにとっても、特徴量の設計・評価・運用に関する体系的な理解は業務の質を大きく向上させるはずです。
ぜひ本記事を通じて、特徴量の本質を掴み、精度の高い機械学習システムを構築するための知識を深めてください。
特徴量の直感と定義:モデルは何を「見て」判断しているのか
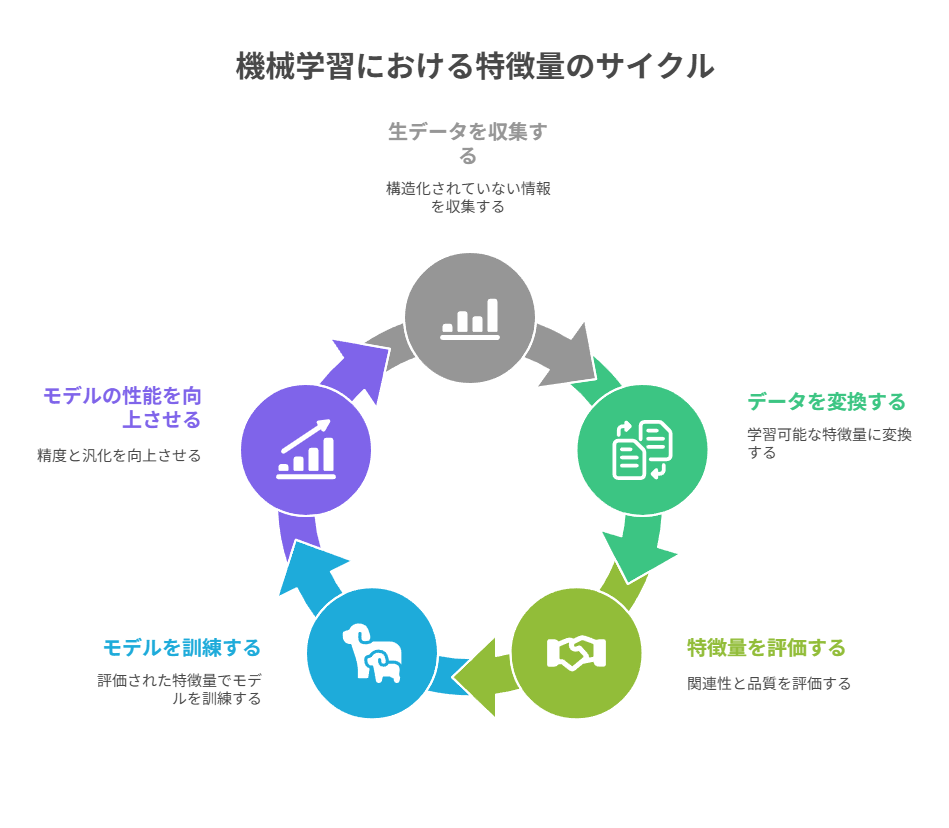

機械学習モデルは生データをそのまま処理するのではなく、学習可能な形に変換された特徴量を通じてパターンを認識します。
良質な特徴量は目的変数との関連性を強調し、ノイズや外れ値の影響を抑える役割を果たします。少ないデータでも規則性を見つけやすくなり、精度と汎化性能が向上します。
不適切な特徴量はモデルの混乱を招き、学習が不安定になる大きな要因となります。
特徴量のイメージ:列=属性=観測
表形式データにおいては、各行が観測(サンプル)、各列が特徴量に相当します。たとえば、以下のような例が挙げられます。
| 特徴量の例 | 説明 | 種類 |
|---|---|---|
| ユーザーの最終ログインからの経過日数 | 直近の利用状況を示す指標 | 派生(差分) |
| 直近30日の購入金額平均 | ユーザーの購買傾向を平滑化した指標 | 派生(集約) |
| 商品価格の対数値 | 歪んだ分布を正規化するための変換 | 高次(非線形変換) |
このように特徴量は「属性」であり、その加工度合いによって以下のように分類されます。
- 生特徴(Raw):加工されていない元のデータ(例:年齢、購入金額)
- 派生特徴(Derived):差分、比率、集約などから作られる(例:直近購入金額の平均)
- 高次特徴(Higher-order):交互作用項や非線形変換を含む(例:年齢×収入、対数変換後の金額)
どの粒度で特徴量を設計するかは、課題の種類やモデル特性、データ分布(スケール・歪度・欠損率)に大きく依存します。
特徴量・ラベル・パラメータ・ハイパーパラメータの違い
機械学習の文脈では似た概念が多いため、混同しやすい用語を整理しておきましょう。
| 概念 | 役割 | 例 |
|---|---|---|
| 特徴量 (X) | モデルが予測の根拠とする説明変数 | 年齢、購買履歴、クリック数 |
| ラベル (y) | 予測対象となる目的変数 | 住宅価格、解約有無、売上高 |
| パラメータ | 学習を通じて最適化される内部の値 | 線形モデルの係数、決定木の分岐条件 |
| ハイパーパラメータ | 学習前に人が設定する制御変数 | 正則化強度、木の深さ、学習率 |
改善の順序は「データ理解 → 特徴量設計 → 検証設計 → モデル・ハイパーパラメータ調整」です。十分な特徴量がない状態でチューニングを繰り返しても、過学習や評価の不安定性が残りやすいため注意が必要です。
特徴量空間と次元の概念(スパース vs デンス)
特徴量は次元数や表現方法によって、モデルの適性が大きく変わります。
One-Hotエンコーディングのような高次元スパース表現は、線形モデルや決定木系アルゴリズムでは扱いやすい一方で、距離や類似度に敏感なアルゴリズム(k近傍法、クラスタリング、ニューラルネットワーク)では不利に働くことがあります。
埋め込み表現(Embedding)や統合統計量によるデンス表現は、次元を抑えつつ意味的な近さを保持できるため、距離ベースの手法やディープラーニングで効果的に機能します。
次元が過剰に高い場合、特徴量空間が疎になり、偶然の一致が増えることで汎化性能が崩れる「次元の呪い」が発生するリスクもあります。
この問題に対する代表的な対策は以下の通りです。
- PCAやUMAPなどによる次元削減
- 低頻度カテゴリの枝刈りやまとめ
- ターゲットエンコーディングにおける正則化の導入
- ドメイン知識に基づいた特徴量選択
適切な次元管理は、過学習を防ぎつつモデルの解釈性と精度を高める重要なステップです。
特徴量設計の基本フロー:仮説 → 生成 → 検証 → 改善
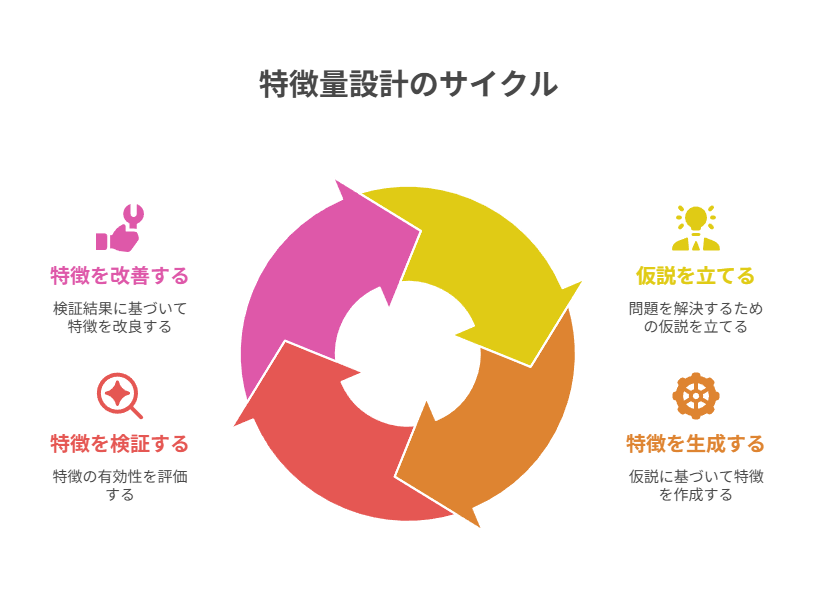

特徴量設計は「数を増やせば良い」という単純な作業ではなく、課題に基づいた仮説検証型のプロセスが求められます。
思いつきで大量に特徴を作成してしまうと、モデルの複雑化や保守コストの増加につながり、かえって精度や安定性を損なうことがあります。
仮説に基づいて最小限の実験を素早く回し、結果を基に改善を繰り返すことが、精度向上と運用容易性の両立に直結します。
課題理解と仮説立案(ドメイン知識 × EDA)
最初のステップは、ビジネス上の目的と機械学習の評価指標を一致させることです。
ユーザー単位、商品単位、セッション単位など、意思決定の粒度を固定することで、後続の特徴量設計や検証が明確になります。探索的データ分析(EDA)で分布の偏り、特徴間の相関、時系列における周期性やトレンド、欠損データのパターンを把握します。
ドメイン知識から行動仮説を導き出すことが重要です。例えば「購買直前は閲覧頻度が増加する」「延滞直前は入金サイクルが乱れる」など、現象に基づく仮説を列挙し、それを検証可能な特徴量アイデアに翻訳します。
生成・前処理(欠損/外れ値/スケーリング)
仮説を特徴量に落とし込む生成と前処理を行います。
欠損値は単なるノイズではなく、意味を持つ場合があります。「欠損フラグ」を作成した上で、中央値やカテゴリ別の代表値で補完します。
外れ値については、ビジネス上の異常行動なのか、データ収集上のエラーなのかを見極める必要があります。場合によってはWinsorize(外れ値を一定の範囲に丸める処理)や対数変換で影響を緩和します。
スケーリングについては、線形回帰や距離ベースのアルゴリズムでは標準化が必須ですが、決定木系では必須ではないものの安定性向上につながる場合があります。再現性を担保するために、前処理は必ず関数化し、学習と推論で同じ処理が適用されるようにします。
検証設計(ホールドアウト/K-Fold/時系列CV)
特徴量の価値を正しく評価するには、適切な検証設計が不可欠です。
誤った検証設計はリーク(未来情報の混入)を引き起こし、過大評価につながります。同一ユーザーが学習データと検証データにまたがらないようにする、時系列データは時間順を考慮したスライスを行うなど、データ構造に応じた分割方法を採用します。
一般的には以下のような手法が用いられます。
| 手法 | 特徴 | 適用シナリオ |
|---|---|---|
| ホールドアウト | データを一度だけ学習用と検証用に分割 | データ量が多い場合のベースライン検証 |
| K-Fold Cross Validation | データをK分割し、学習と検証を繰り返す | 汎化性能を安定的に測定したい場合 |
| 時系列CV | 時間順にデータをスライスして学習・検証 | 金融・需要予測など時系列依存が強い場合 |
分類問題では閾値最適化やコストに応じた評価指標(精度・再現率・F1・AUCなど)を組み合わせることが重要です。検証の粒度は最終的な運用の意思決定単位と揃えることが推奨されます。
反復改善(重要度・SHAP・エラーパターン分析)
特徴量設計は一度で完成するものではなく、反復的な改善が必須です。
単なる特徴量重要度の順位に依存するのではなく、部分依存図(PDP)やSHAP値を用いて、特徴量の影響が単調か、閾値が存在するか、他の特徴との相互作用があるかを確認します。
誤分類や大きな誤差が出たサンプルを分析し、どの特徴が不足しているのかを具体化します。過学習の兆候(fold間のスコアばらつき拡大、特定外れ値への依存)が見られた場合は、特徴量の正則化やシンプル化で対処することが求められます。
運用前チェック(データ/概念ドリフトの監視計画)
学習済みモデルを本番環境に導入する際には、特徴量の安定性を監視する仕組みが不可欠です。
具体的には、PSI(Population Stability Index)やKLダイバージェンスを用いた分布監視、スキーマの破壊検知、データ到着遅延のチェックなどが挙げられます。
概念ドリフトに対応するために、定期的なリトレーニングの頻度やリスコアリングの戦略、予測閾値の再最適化計画をあらかじめ設計しておきます。どの指標を監視し、どのレベルでアラートを出すかを事前に関係者と合意しておくことで、運用後の保守作業が大幅に効率化されます。
特徴量設計の基本パターンと実例まとめ
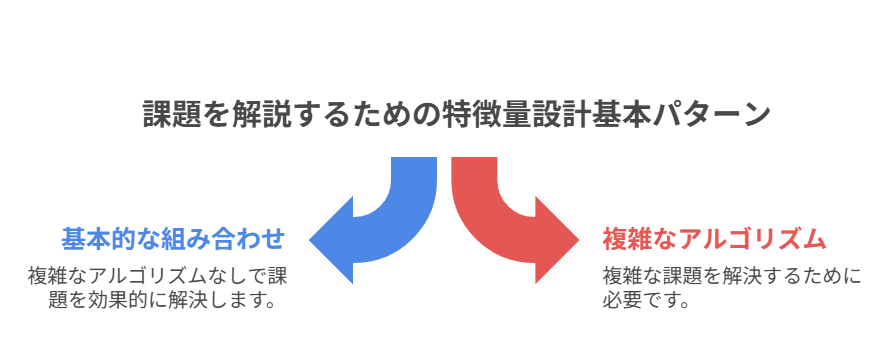

多くの機械学習課題は、複雑なアルゴリズムを導入するよりも、基本的な特徴量設計の型を適切に組み合わせることで十分に解けるケースが多くあります。
むやみに高度な手法に頼るのではなく、まずは「勝ちパターン」を素早く適用し、必要に応じて精緻化することが精度向上と開発効率の両面で有効です。ここでは代表的な特徴量設計パターンとその実務での活用例を整理します。
交互作用・組み合わせ・統計量(平均/分散/順位)
交互作用特徴量は、複数の変数を掛け合わせることで非線形な関係を顕在化させます。
例えば「価格×数量」は単なる売上高として利用でき、購買行動を直接的に説明します。集計統計量(平均・分散・順位など)は安定した基準を提供し、外れ値の影響を軽減します。順位(パーセンタイル変換)はスケールの異なる変数を比較可能にするため、異分布データの分析に特に有効です。
| 特徴量パターン | 例 | 効果 |
|---|---|---|
| 交互作用 | 価格 × 数量 | 非線形関係の顕在化、購買力の把握 |
| グループ平均 | ユーザーごとの平均購入額 | 安定した基準線、外れ値抑制 |
| 分散 | アクセス時間の分散 | 行動の安定性・変動性を測定 |
| 順位(パーセンタイル) | 商品価格の分布内順位 | スケール非依存、異分布比較に有効 |
カテゴリ同士の組み合わせは次元爆発を引き起こしやすいため、低頻度カテゴリの除外やターゲットエンコーディングによる圧縮が推奨されます。
正規化/標準化/ロバストスケーリングの使い分け
スケーリングはモデルの性質やデータ分布に応じて適切に選択する必要があります。
| 手法 | 特徴 | 適用モデル・状況 |
|---|---|---|
| 正規化(0–1スケーリング) | 最小値を0、最大値を1に変換 | 距離ベース(k-NN, K-means)、ニューラルネットワーク |
| 標準化(Z-score) | 平均0、分散1に変換 | 線形回帰、SVM、ロジスティック回帰(係数解釈性向上) |
| ロバストスケーリング | 中央値とIQRを基準にスケーリング | 外れ値が多いデータセット(金融、不正検知など) |
どのスケーリング手法を用いるかは、アルゴリズムの特性・誤差指標の性質・外れ値の有無によって決まります。適切なスケーリングは収束速度を高め、予測精度の安定化に寄与します。
次元削減(PCA/UMAP)と情報圧縮の効果
高次元データは計算コストや過学習のリスクを高めるため、次元削減による情報圧縮が効果的です。代表的な手法は以下の通りです。
| 手法 | 特徴 | 主な利用シーン |
|---|---|---|
| PCA(主成分分析) | 分散を最大化する線形変換に基づく圧縮 | ノイズ除去、計算負荷軽減、線形モデルの前処理 |
| UMAP | 局所構造の保持に優れた非線形次元削減 | クラスタリング前処理、可視化、非線形パターンの発見 |
これらを用いて得られた圧縮後の成分を特徴量としてモデルに投入すると、疎なスパース表現の過学習を抑制し、予測の平滑化や解釈性向上につながります。特にUMAPはクラスタ構造の把握に強く、探索的データ分析のフェーズでも有用です。
モデルとの相性:アルゴリズム別の特徴量戦略


同じ特徴量でも、アルゴリズムごとにその効果の出方は大きく異なります。あるモデルでは有効に働く特徴量が、別のモデルではノイズになることもあります。
前処理のコストや推論要件を踏まえつつ、最短で性能を引き出せる組み合わせを選ぶことが重要です。以下では代表的なアルゴリズムごとに有効な特徴量戦略を整理します。
線形モデル(L1/L2)に効く前処理とスパース設計
線形回帰やロジスティック回帰は特徴量と目的変数の線形関係を前提としています。標準化や外れ値緩和、単調変換(対数変換、平方根変換など)によって線形性を強化することが基本戦略となります。
L1正則化(Lasso)は特徴量選択に強い一方で不安定性があるため、相関の高い特徴量は事前に統合するか、多重共線性を抑える工夫が必要です。スパースかつ高次元な特徴量を扱える点で解釈性に優れ、ベースラインモデルや本番環境でのバックアップモデルとして有用です。
決定木系(LightGBM/XGBoost/CatBoost)で効く離散化・頻度系特徴
勾配ブースティング系アルゴリズムは、単調変換やスケーリングに対してロバストであり、特徴量の分布形状に依存しにくいという強みがあります。
ビン分割やカテゴリ頻度、カウント特徴、順位変換といった離散化・統計的特徴が有効です。特にCatBoostはターゲット統計量を自然に取り込めるため、カテゴリ変数を大量に含むデータで強力です。外れ値への耐性が高く、交互作用を自動的に拾えることから、仮説検証のスピードを加速させる実務的な選択肢となります。
深層学習:表現学習と生特徴の扱い、正規化の考え方
ディープラーニングは表現学習によって、生特徴から複雑な非線形関係を自動的に抽出する力を持ちます。しかし、十分なデータ量がなければ学習が不安定になりやすく、過学習も発生しがちです。Batch NormalizationやLayer Normalization、ドロップアウトなどの正則化が不可欠です。
カテゴリ変数には埋め込みベクトルを割り当てることで、One-Hot表現に比べて次元を圧縮しつつ意味的な関係性を捉えられます。前処理の手間を削減できる一方、推論コストや説明責任(Explainability)の観点から、導入時にはシステム要件を十分に考慮する必要があります。
kNN/SVM/ナイーブベイズの前処理要点
距離や確率に依存するモデルでは、前処理が性能を大きく左右します。
| アルゴリズム | 重要な前処理 | 理由・効果 |
|---|---|---|
| kNN | 標準化、正規化、次元削減(PCAなど) | 距離計算の一貫性を確保し、高次元の疎性による精度低下を防止 |
| SVM | スケーリング、外れ値処理、カーネル選択 | マージン最大化のためにスケールが揃っていることが必須、外れ値で境界が歪むのを防ぐ |
| ナイーブベイズ | 離散化、特徴量の統合 | 条件付き独立の仮定に近づけることで精度が安定しやすい |
特にkNNは特徴量スケールの違いがそのまま距離計算に影響するため、標準化を怠ると性能が著しく低下します。
SVMはカーネル選択に応じて非線形関係を捉えられますが、前処理の質がそのまま決定境界の形状に反映される点に注意が必要です。ナイーブベイズはシンプルなモデルであるがゆえに、仮定に近づける工夫が有効です。
評価と選択:どの特徴量を残すか


特徴量エンジニアリングでは「作るより捨てるほうが難しい」と言われます。不要な特徴量を削ぎ落とすことで、モデルの解釈性や汎化性能を高め、運用コストの削減にもつながります。重要なのは、単なる精度だけでなく、安定性と再現性を基準に特徴量を評価・選択することです。
以下では代表的な評価指標と手法の違いを整理し、実務的な選択基準を解説します。
Permutation/SHAP/ゲイン/分割回数の違いと読み方
特徴量重要度を測る方法はいくつかありますが、それぞれ性質が異なります。
| 手法 | 特徴 | 強み | 注意点 |
|---|---|---|---|
| Permutation Importance | 特徴量をシャッフルして精度低下を測定 | モデル非依存、汎化性能に直結 | 計算コストが高い、大規模データで非効率 |
| SHAP値 | 各予測における特徴量の寄与を定量化 | 局所~大域の説明が可能、可視化に強い | 計算が重い、近似手法の工夫が必要 |
| ゲイン | 木系アルゴリズムで情報利得を測定 | 高速計算、直感的に理解しやすい | バイアスが強く、相関があると過大評価 |
| 分割回数 | 木における特徴量の使用頻度 | 特徴量の利用傾向を把握しやすい | 重要度の強弱は反映されにくい |
複数の指標を組み合わせて評価し、特定の特徴量に過度な依存が見られる場合は、代替特徴の追加や正則化を検討します。
相関・多重共線性(VIF)と特徴選択(逐次/正則化)
高相関な特徴量が多いと、解釈性が損なわれるだけでなく、分散が大きくなり予測が不安定になります。多重共線性はVIF(Variance Inflation Factor)で数値的に測定可能で、VIFが10を超える場合は注意が必要です。
代表的な対策は以下の通りです。
- 代表特徴の選抜:同じ意味を持つ変数群から一つを残す
- 主成分分析(PCA):相関した特徴を射影し次元削減
- 逐次選択(前進/後退):一つずつ特徴を追加/削除して最適集合を探索
- L1正則化(Lasso):不要な特徴を自動的にゼロ化しスパース化
決定木系モデルは相関に比較的強いですが、冗長な特徴が多いと推論時間が増加し、運用負荷につながります。
安定性選択とターゲットリーク検知
特徴選択は一度の試行結果だけでなく、再現性と安定性を評価することが重要です。ブートストラップやクロスバリデーションのfoldを変えて繰り返し特徴選択を行い、選ばれた特徴の一致率を測定することで、安定性を定量化できます。
実務で特に注意すべきはターゲットリークです。訓練時には利用可能でも、予測時には存在しない未来情報が特徴量に含まれていると、学習時のスコアは高くても本番では使えないモデルが出来上がってしまいます。典型例としては「集計期間の不一致」「目的変数を暗黙に含むフラグ変数」があります。
疑わしい特徴量は意図的に除外して再学習し、性能差を比較することで影響を検証することが推奨されます。信頼性の高い特徴量セットを構築でき、長期的に安定したモデル運用が可能になります。
まとめ


本記事では、機械学習における特徴量の重要性とその設計プロセスを一貫して整理しました。
特徴量はモデルが「世界を理解するための語彙」であり、単なる入力データではなく、精度・再現性・運用コストを左右する最も重要な要素です。効果的な特徴量設計は、仮説立案から生成・前処理、検証設計、反復改善、運用監視に至るまで、体系的なプロセスを経て行う必要があります。
基本パターン(交互作用・統計量・スケーリング・次元削減など)を適切に組み合わせることで、多くの課題に対応可能であることを示しました。アルゴリズムごとの相性を理解し、線形モデル、決定木系、ディープラーニング、距離・確率ベースの手法に最適な特徴量戦略を選ぶことが、効率的な性能向上につながります。
特徴量の評価・選択ではPermutationやSHAPなどの指標を組み合わせて活用し、相関やターゲットリークに注意しながら、安定性の高い特徴量セットを構築することが重要です。作成した特徴量をどれだけ精緻に選別できるかが、モデルの信頼性と長期的な運用成功を決定づけます。
特徴量設計は「芸術と科学の融合」とも言われる領域です。正しいプロセスとパターンを理解し、業務ドメインの知識と組み合わせることで、汎化性能の高いモデルを効率的に構築できるでしょう。



